大部分量化基金都是骗人的-伍治坚的财新博客-财新网

导读

· 如何辨别好的和差的量化交易策略？

· 运气对于基金经理的投资回报有多大作用？

· 如何防止自己把钱交给一个“猴子”管理？

· 为什么说大部分量化基金经理都是骗人的？

随着计算机编程在金融投资中得到越来越广泛的应用，量化交易也越来越得到大家的关注。据华尔街日报报道，在过去20年，量化基金的数量和管理的资产规模有了大幅度增长。股票指数期货交易中，超过7成为量化交易。国际外汇期货交易中，量化交易量大约占到8成以上。

那么到底什么是量化交易？它和传统的基金投资策略有何不同？依靠电脑程序进行投资，和人相比有什么优劣点？如何判断一个量化交易策略的好坏？带着这些问题，我和美国杜克大学的坎贝尔·哈维（Campbell Harvey）教授进行了一场非常有趣的谈话。

由于我们谈话涵盖的范围比较广，因此我将我们的谈话内容分为两篇文章分别发表。今天这篇文章，是我们谈话的第一部分，主要讲讲如何来甄别量化投资策略的好坏。

首先向大家介绍一下坎贝尔·哈维教授。哈维教授是美国杜克大学的金融学教授。他是2016年美国金融协会的主席。哈维教授在公司治理，行为金融，计量经济，计算机科学等领域发表过120多篇顶级学术论文。他写的关于甄别基金经理的运气和技能的文章，连续两年获得Journal of Portfolio Management最佳论文奖。他也曾8次获得美国金融分析师协会（CFA）颁发的格雷厄姆/多徳奖（Graham/Dodd Awards）。

我们从哈维教授写过的一篇论文《Evaluating Trading Strategies》说起。

我问哈维教授，在其他一些领域，比如物理，确认一个新发现需要达到“5倍标准差”。但是为什么这个标准在金融研究里没有被执行？业界好像满足于“2倍标准差”标准。

对于这些统计学概念不太熟悉的朋友，让我在这里稍微为大家做一下科普。

在统计学上，如果我们要确认任何规律或者发现，确保该发现具有统计意义，那么我们就需要计算该发现的T值和P值。

如果T值为2左右（1.96），那么其对应的P值（假设自由度够大）就为0.05左右。也就是说，该统计结果有效的概率为95%。这也意味着，在这种情况下得到的统计结果，有5%的概率是假象。这个标准，称为“2倍标准差”要求。

在一些精确度要求比较高的计算和实验中，“2倍标准差”的误差率太高，因此实验人员需要提高确认结果的门槛，到3倍，甚至5倍标准差。

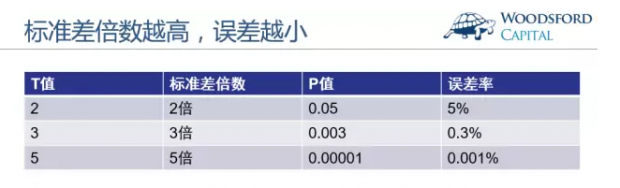
从上表中我们可以看到，T值越大，P值越小，结果产生误差的概率也越小。如果一个发现的T值达到5，也就是“5倍标准差”，那么该结果有效的概率为99.999%。因此，标准差倍数越高，T值越高，实验结果越可信。

在哈维教授的文章中，他提到了希格斯玻色子（也被称为“上帝粒子”）的例子。

早在1960年代，英国科学家彼得·希格斯就从理论上提出“希格斯玻色子”存在的可能性。但是，在实验中真正确认该粒子的存在，则一直要等到2013年。

2010年，意大利物理学家托马索·多里戈宣称，美国费米实验室的万亿电子伏加速器（Tevatron）可能已经发现了希格斯玻色子。但当时的发现仅限于3倍标准差，因此没有在科学界获得认可。

直到2013年，欧洲核子研究组织确认发现希格斯玻色子时，其发现的可靠性达到了5倍标准差。因此这些物理学家们才敢向世界大方宣布，我们终于证实了“上帝粒子”的存在。

为什么2倍标准差和5倍标准差相差很大？原因在于，科学家们为了寻求某一种发现，他们可能会试上成千上万次实验。以希格斯玻色子为例，理论上该粒子仅会在每 100亿次碰撞中产生一次。因此为了证实希格斯玻色子的存在，物理学家们设计的粒子对撞机需要重复上千万亿次数级别的碰撞。

在任何实验中，都有运气的成分，因此也可能会导致虚假的发现。重复实验的次数越多，偶然碰到假象的概率也越高。这就是为什么物理学家们需要把检验标准提高到5倍标准差，确保该实验结果在统计学上能够过关的原因所在。

“5倍标准差”规则，背后有非常强的逻辑性。但是这个规则，并没有被金融研究行业采纳。目前绝大部分的金融量化研究，都还是以“2倍标准差”作为接受实验结果的标准。这就导致很多金融研究得出的结论并不一定经得起推敲。

在哈维教授写的论文中，他提到了一个非常有趣的例子。

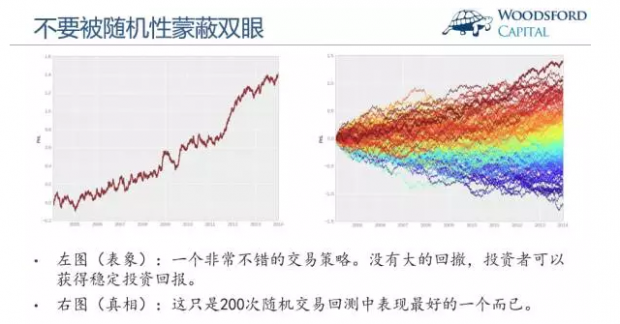
如果一家基金向投资者呈现如上图中左边那张回测业绩，相信绝大多数投资者都会非常喜欢这个交易策略。该投资策略有非常稳定的投资表现，几乎没有任何大幅度的回撤。即使在2008年金融危机期间都有不俗的表现。很多投资者可能会当即拍板：我决定投100万！

但事实的真相从右边那张图中浮现出来。原来，研究人员只是做了200次随机回测，然后从中挑选出一个表现最好的策略而已。对于投资者来说，他只看到那一个最好的策略回报，并没有看到其他199个表现更差的情况。由于这所有200个交易策略都是随机产生的，因此其未来的投资回报完全不可能重复。投资者接下来的投资回报和左图一样的概率几乎为零。

这个简单的例子告诉我们：即使没有任何技能，只要样本量足够大，也能够产生足以“以假乱真”的投资业绩。

有些朋友可能对上文提到的统计知识点不太理解。那么让我在这里再和大家分享一个更为简单易懂的例子。

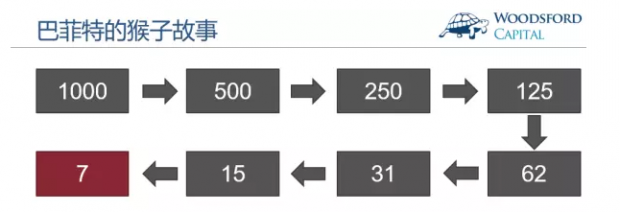
假设有1000只猴子参加扔硬币大赛。如果扔到“正面”，猴子可以继续留下来参加下一轮。如果扔到“反面”，该猴子被淘汰出局。大致来说，每一轮会有一半猴子被淘汰。我们可以看到，在扔硬币大赛连续进行了7轮后，大约会剩下7只猴子。

如果我们去检验这7只猴子的扔硬币记录，每只猴子都连续扔到7次硬币的正面。任何一个人，连续扔到7次正面的概率都是很小的。因此他会告诉你，这和运气完全无关，而是我有一套扔硬币的“秘笈”。聪明的读者，你会相信一只猴子有扔硬币的“特殊技能”么？

当我向哈维教授提到这个例子时，他完全赞同我的意见。哈维教授说到，如果有10,000个基金经理，那么在10年后，大约有10个基金经理会连续10年跑赢大盘战胜市场。这完全是随机和运气决定的，和基金经理们的技能一点关系都没有。这10个基金经理一个个看起来都像股神。

这就是哈维教授在论文中想要表达的意思：金融行业目前使用的统计学标准，比其他科学性强的行业落后太多。我们需要提高金融行业确认投资业绩可靠性的标准。哈维教授提议，把 “2倍标准差”提高到“3倍标准差”。提高了标准，就能够把仅凭运气而获得的投资回报的策略和基金经理排除在外，也能降低投资者买到一只“猴子”基金的概率。

那么作为普通投资者，如何提高自己的鉴别能力，降低自己买到“猴子基金”的概率呢？

哈维教授提到，在业界，当很多机构去分析任何一个量化策略时，有一个不成文的规定，叫做“夏普率减半”，即把对方提供的夏普率减掉一半。换句话说，如果一个量化策略在回测中显示可以获得每年10%的投资回报。那么作为投资者，你应该期望该策略在接下来的实际交易中，带来每年5%的投资回报。

这主要是因为，量化基金经理提供给投资者看的投资回报，都是他们在经过成百上千次回测后挑选出来的最好的那个策略。为了防止自己碰到一只特别幸运的“猴子”，投资者需要做出一定“缩水”调整。

用这种简单粗暴的方法调整夏普比率，很多人可能会觉得不够科学。基金经理会说，这对我不公平。有些投资者也会说，这会不会导致我们错过原本非常不错的交易策略。因此在哈维教授的论文中，他提到了一个更加科学的调整夏普比率（Sharpe Ratio Haircut）的方法。

对于那些非金融背景出身的朋友，让我在这里稍微花点时间给你们科普一下涉及的专业概念。

如上图所示，夏普比率（Sharpe Ratio），是用超额回报（投资回报减去无风险利率），然后再除以投资组合的波动率（标准差）。该比率主要衡量的是“风险调整后收益”。

为了省事，你基本只要记住：夏普比率越高，说明该投资策略越好。（注：这是针对非金融行业读者，比较简单粗暴的解释方法。真要细究的话，需要仔细分析夏普比率是怎么得出来的。这已经超出了本文的范围，因此不再赘述。）

绝大部分比较专业的金融机构和基金，都会向投资者披露该投资策略（或者基金）的夏普比率。哈维教授在他的论文中提出，我们应该对金融机构向我们展示的夏普比率保持怀疑态度，并进行合理的调整。

具体的调整细节涉及一些统计知识。我在这里稍微给大家分享一下，有兴趣的朋友可以去阅读哈维教授的原著。在哈维教授的论文中，他甚至提供了计算机程序源代码，有兴趣的朋友可以直接下载然后使用。

假设某基金的夏普比率为0.92，该基金来自于一个包含200个类似基金的数据库。那么我们根据其夏普比率，算出其P值（0.4%）。然后根据样本数量，调整其P值。在调整过的P值下，我们再计算出调整后的夏普比率为0.08，比原来的夏普比率下降了91%。

这个简单易用的方法，可以帮助我们去除一些基金在宣传材料中显示的夏普比率的“水分”，让投资者获得更加真实客观的信息。

我向哈维教授提出，美国和中国量化研究的一大区别是，美国的金融历史数据量要丰富得多。美国的股市数据，可以追溯到1920年代。而中国的A股，只是 1990年代刚刚开始。中国第一只公募基金，一直要等到2001年才开始发售。这是不是意味着绝大部分基于中国市场的量化策略都很难通过严格的统计要求？

哈维教授的看法是：大致来讲，确实数据越多，量化策略的可靠性越高。毕竟如果一个量化策略基于的样本量很小，那么其结果就可能有很强的偶然性，因此难以在未来复制。

对于像中国这样的新兴市场，有两个方法可以提高量化策略的质量。首先是增加样本量。由于数据历史有限，不可更改，因此研究人员只能在数据频度上做文章。比如将研究的数据频度调到每日股价变动，每小时股价变动甚至是每分钟股价变动。频度越是密，其数据量就越大。

其次，如果一些策略在发达国家中得到验证可行，那么我们就可以考虑把这样的策略移到像中国这样的新兴市场进行交易。由于在其他国家市场中已经被验证可行，因此类似策略在中国也行得通的可能性要高很多。

这让我想起了之前我和许仲翔（Jason Hsu）先生做过的一篇专访，专门讨论聪明贝塔策略在中国市场的可行性。有兴趣的朋友可以搜索“伍治坚”+关键词“聪明贝塔”找到该文章。

我向哈维教授提出，虽然巴菲特通过“猴子”的例子提醒投资者不要被基金经理表面的业绩误导，但他同时也指出，有很多好的基金经理都来自于同一个村落，即所谓的“价值投资”村落。在一次公开演讲中，巴菲特举了不少这样的基金经理的例子，包括Walter Schloss, Tom Knapp，以及他自己。这些经理未必能够达到“3倍标准差”或者更高的统计要求，但是他们都是很优秀的基金经理。

这个例子是否说明，投资者们在选择基金经理时，也需要结合考虑该经理的投资风格和哲学来做出判断？

哈维教授表示赞同。挑选好的基金经理，区分该基金经理的回报是来自于运气还是技能，是一件非常复杂的系统工程。很多大型机构，比如养老基金，国家主权基金等都做不好，可见其难度之高。哈维教授在这个领域写的好几篇文章，被评为年度最佳论文，为这方面的研究做出了贡献。但事实上，能够真正读懂并理解他文章的人，仅限于少数的业内人士。这本身就凸显了要想挑选好的基金经理，难于上青天的事实。可笑的是，很多个人投资者“无知者无畏”，反而觉得选基很容易，这实在让人有些哭笑不得。

目前的中国，大约有3,000个左右公募基金，3,000多个私募基金。在美国，大约有9,000多个公募基金。在如此众多的基金基数上，要想找出几个基金连续5年，或者更长时间取得好的投资回报，并不是一件难事。甚至这些基金经理可能完全不需要任何技能，仅凭运气，也能连续多年获得好的回报。而对于投资者来说，他以为自己买到了一个非常好的基金，其实只不过是把钱交给了一只幸运的猴子而已。

我向哈维教授请教，在这种情况下，我们普通投资者应该怎么做？特别是我们很多投资者一没有专业知识，二没有数据信息。在这种情况下去挑选主动型基金，岂不是相当于误打误撞靠天吃饭？我们是不是应该放弃幻想，满足于购买那些低成本的指数基金？

哈维教授表示完全赞同。在他看来，中国的3,000个公募基金，至少一半达不到专业的技能标准，根本不值得投资。美国的情况更遭。在哈维教授写的另一篇论文中，他们发现在美国，最多只有10%的公募基金经理有真正的投资技能。

对于普通个人投资者来说，他们大部分人都有自己的本职工作，同时并非来自金融专业。这些投资者，没有时间，没有专业技能，也没有数据信息帮助他们去挑选基金。因此对于他们来说，更好的选择是购买低成本的指数基金。

在哈维教授写的《Evaluating trading strategies》一文中，他得出结论：

Most of the empirical research in finance, whether published in academic journals or put into production as an active trading strategy by an investment manager, is likely false. Half the financial products that companies are selling to clients are false.

翻译：绝大部分在金融期刊上发表，或者向投资者兜售的主动型量化交易策略，都可能是骗人的。基金公司们售卖的投资产品，有一半都是“假货”。

希望投资者们可以从哈维教授的研究中学到一些有用的知识，提高自己的警惕程度，不要轻易堕入基金公司和理财机构的销售陷阱，做出最有利于自己的理性投资决策。

【注：我和哈维教授的谈话摘要第二部分，主要涉及到人工智能，机器学习（Machine Learning）等在量化交易中的应用。我会在另一篇文章中做出总结。】

要想听伍治坚的电话录音，请在喜马拉雅FM/蜻蜓FM/itune Podcast中搜索“伍治坚证据主义”。

伍治坚是《小乌龟投资智慧：如何在投资中以弱胜强》的作者。在京东，淘宝或者当当搜索书名或者作者名，都可以购买到该书。